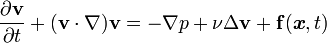Quer ser milionário? Basta resolver um dos problemas matemáticos do milênio

Já pensou em ficar milionário do dia para a noite? Que tal resolver um dos problemas não resolvidos da matemática!

No ano 2000, o Clay Mathematics Institute ofereceu um prêmio para quem conseguisse resolver um dos sete dos maiores problemas não resolvidos da matemática. O valor do prêmio é de  US $ 1 milhão por problema. Até à data, apenas um dos sete problemas foi resolvido. Os sete problemas são chamados de Problemas do Prémio Millennium. São eles:

1 - Problema P = NP

O problema "P versus NP" é o principal problema aberto da Ciência da Computação. Possui também enorme relevância em campos que vão desde a Engenharia até a criptografia aplicada aos serviços militares e às transações comerciais e financeiras via Internet.  Foi essencialmente mencionado pela primeira vez em 1956 uma carta escrita por Kurt Gödel com John von Neumann. Gödel perguntou se um determinado problema NP completo poderia ser resolvido em tempo quadrático ou linear

2 - A conjectura de Hodge

A conjectura de Hodge é um importante problema, ainda não resolvido, de geometria algébrica no que diz respeito a atopologias de variedade algébrica complexa não singular e as subvariedades dessa variedade. 

Concretamente, a conjectura propõe que certos grupos de co-homologia de Rham são algébricos, isto é, são somas de dualidades de Poincaré de classes homólogas de subvariedades.

3 - A conjectura de Poincaré (resolvido em 2010 por Grigori Perelman)

A conjectura de Poincaré afirma que qualquer variedade tridimensional fechada e com grupo fundamental trivial é homeomorfa a uma esfera tridimensional. Ou seja, a superfície tridimensional de uma esfera é o único espaço fechado de dimensão 3 onde todos os contornos ou caminhos podem ser encolhidos até chegarem a um simples ponto

Esta conjectura surgiu na seqüência de uma outra conjectura formulada por Henri Poincaré em 1900, que afirmava que qualquer variedade tridimensional fechada e com homologia trivial (denominada uma esfera de homologia) era homeomorfa a uma esfera. Na verdade esta conjectura foi refutada pelo próprio Poincaré em 1904, que forneceu o primeiro exemplo de uma esfera de homologia não homeomorfa a uma esfera.

Resolução

Na edição publicada em 27 de agosto de 2006 do jornal britânico da BBC, foi noticiada a resolução do problema da Conjectura de Poincaré ao matemático russo Grigori Perelman. Em 18 de março de 2010, o Clay Mathematics Institute anunciou que o Dr. Grigori Perelman era o vencedor de um dos sete Problemas do Prémio Millenium. Mas o matemático se recusou a ganhar o prêmio de um milhão de reais, bem como a Medalha Fields (equivalente ao Prêmio Nobel de Matemática), alegando que o seu maior prêmio foi a resolução do problema.

4 - A hipótese de Riemann

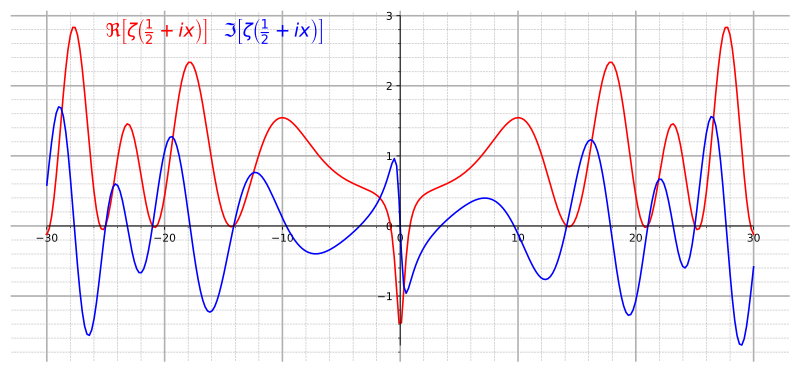Gráficos das partes real (a vermelho)
 e imaginária (a azul) da linha crítica
da função zeta de Riemann.

A hipótese de Riemann é uma hipótese (ou conjectura) matemática, publicada pela primeira vez em 1859 por Bernhard Riemann, que declara que os zeros não-triviais da função zeta de Riemann pertencem todos à "linha crítica":

onde  denota a parte real de s.

Os zeros triviais da função zeta de Riemann são os inteiros negativos pares: .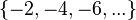

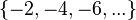5 - A existência de Yang-Mills e a falha na massa

Este problema é um dos requisitos para a prova matemática da teoria quântica de campos de acordo com o modelo padrão de partículas fundamentais e ainda continua sem solução.

O problema consiste na prova com todo o rigor matemático característico da física matemática contemporânea. O vencedor também deve provar que a massa da menor partícula fundamental predita pela teoria quântica de campos seja positiva, ou seja, a partícula precisa possuir um intervalo de massa.

6 - A existência e suavidade de Navier-Stokes

As Equações de Navier-Stokes são um dos pilares da mecânica de fluidos. Estas equações descrevem o movimento de um fluido (líquido ou gás) no espaço físico.

As soluções das equações de Navier-Stokes são utilizadas em diversas aplicações práticas, entretanto, o entendimento teórico destas soluções são incompletos. Particularmente, geralmente as soluções destas equações incluem turbulência, as quais se mantem como um dos maiores problemas em aberto da física, apesar de sua imensa importância para a física teórica e a engenhara.

Na matemática, as equações de Navier-Stokes são um sistema não linear com equação de derivadas parciais para campos de vetores abstratos de qualquer tamanho. 

7 - A conjectura de Birch e Swinnerton-Dyer

A conjectura de Birch e Swinerton-Dyer foi enunciada em 1965 e estabelece uma condição para que uma curva algébricaplana, f(x,y) = 0, definida sobre os racionais — isto é, com os argumentos x,y∈ℚ—, tenha infinitos pontos racionais —isto é, (x,y) solução de f(x,y) = 0, com x,y∈ℚ—, como por exemplo a circunferência.

Referências:

•  Rob Womersley, Parabola Volume 37, Issue 2 (2001)m The Travelling Salesman Problem and Computational Complexity
• Hodge, W. V. D. "The topological invariants of algebraic varieties". Proceedings of the International Congress of Mathematicians, Cambridge, MA, 1950, vol. 1, pp. 181–192.
• Mackenzie, Dana (2006-12-22). "The Poincaré Conjecture--Proved". Science(American Association for the Advancement of Science) 314 (5807): 1848–1849
• Arthur Jaffe & Edward Witten. "Quantum Yang-Mills theory." Official problem description (em inglês) Clay Mathematics Institute.
• Ladyzhenskaya, O.. The Mathematical Theory of Viscous Incompressible Flows (em inglês). 2 ed. New York: Gordon and Breach, 1969.
•  Wiles, Andrew (2006). "The Birch and Swinnerton-Dyer conjecture". In Carlson, James; Jaffe, Arthur; Wiles, Andrew. The Millennium prize problems. American Mathematical Society. pp. 31–44. ISBN 978-0-8218-3679-8.